Simulez vos placements!
Calculatrice d’Intérêt Composé
Si vous cherchez d’autres simulateur financier n’hésitez pas à consulter ces pages : Inflation: Comment l’Utiliser ? / Comment calculer un prêt immobilier ?
Sommaire
Comprendre les intérêts composés
La capitalisation est le processus par lequel les revenus d’un investissement sont réinvestis pour générer encore plus de revenus. C’est un concept clé pour maximiser la rentabilité à long terme. Par exemple, si vous investissez 10 000 € à un taux d’intérêt annuel de 5 % et que vous réinvestissez les intérêts chaque année, votre capital augmentera de manière exponentielle.
En effet, les intérêts venant gonfler le capital, la base de calcul des intérêts devient chaque année encore plus importante, permettant de générer encore plus d’intérêts ! C’est l’effet boule de neige et c’est très puissant ! C’est la base de toute gestion patrimoniale. Si vous ne prenez pas en compte ce point pour votre propre épargne, vous n’arriverez jamais à vous assurer l’avenir radieux dont vous rêvez !
Exemple Chiffré
Reprenons notre exemple : vous investissez 10 000 € à un taux d’intérêt annuel de 5 %, composé annuellement. Cela signifie que vous réinvestissez les gains chaque année et que vous recalculez les intérêts sur une somme d’argent plus importante. Voici comment cela fonctionne :
| Année | Calcul | Capital |
| 0 | 10 000 € | |
| 1 | 10 000 * 1.05 = 10 500 € | 10 500 € |
| 2 | 10 500 * 1.05 = 11 025 € | 11 025 € |
| … | ||
| 10 | 15 513,28 * 1.05 = 16 288,95 € | 16 288,95 € |
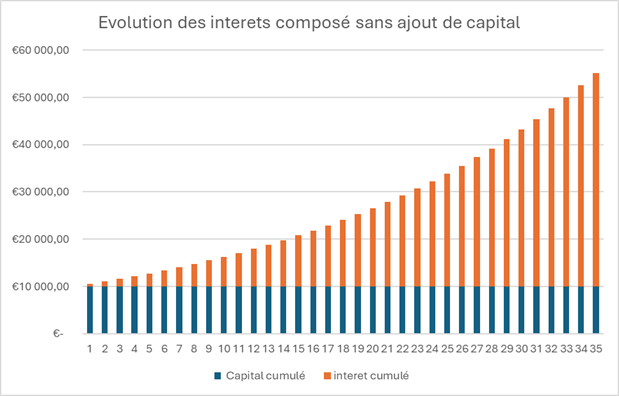
Année après année, les intérêts générés viendront s’ajouter à votre capital initial. Ce capital accru produira à son tour des intérêts plus importants, et ainsi de suite. Ce mécanisme d’intérêts composés se poursuivra jusqu’à ce que, chaque année, le montant des intérêts dépasse celui du capital initialement investi.
Vous percevez la puissance des intérêts composés ? L’augmentation de votre gain sera de plus en plus importante au regard de l’investissement initial et du cumul d’intérêts obtenu, et tout ça avec une mise de départ fixe. Vous ne me croyez pas ? Alors faisons une projection un peu plus longue !
| Année | Ajout capital | Capital cumulé | Total gain | Intérêt | Intérêt cumulé |
| 1 | 0 | 10 000,00 € | 10 500,00 € | 500,00 € | 500,00 € |
| 2 | 0 | 10 000,00 € | 11 025,00 € | 525,00 € | 1 025,00 € |
| 3 | 0 | 10 000,00 € | 11 576,25 € | 551,25 € | 1 576,25 € |
| 4 | 0 | 10 000,00 € | 12 155,06 € | 578,81 € | 2 155,06 € |
| 5 | 0 | 10 000,00 € | 12 762,82 € | 607,75 € | 2 762,82 € |
| 6 | 0 | 10 000,00 € | 13 400,96 € | 638,14 € | 3 400,96 € |
| 7 | 0 | 10 000,00 € | 14 071,00 € | 670,05 € | 4 071,00 € |
| 8 | 0 | 10 000,00 € | 14 774,55 € | 703,55 € | 4 774,55 € |
| 9 | 0 | 10 000,00 € | 15 513,28 € | 738,73 € | 5 513,28 € |
| 10 | 0 | 10 000,00 € | 16 288,95 € | 775,66 € | 6 288,95 € |
| 11 | 0 | 10 000,00 € | 17 103,39 € | 814,45 € | 7 103,39 € |
| 12 | 0 | 10 000,00 € | 17 958,56 € | 855,17 € | 7 958,56 € |
| 13 | 0 | 10 000,00 € | 18 856,49 € | 897,93 € | 8 856,49 € |
| 14 | 0 | 10 000,00 € | 19 799,32 € | 942,82 € | 9 799,32 € |
| 15 | 0 | 10 000,00 € | 20 789,28 € | 989,97 € | 10 789,28 € |
| 16 | 0 | 10 000,00 € | 21 828,75 € | 1 039,46 € | 11 828,75 € |
| … | … | … | … | … | … |
| 32 | 0 | 10 000,00 € | 47 649,41 € | 2 269,02 € | 37 649,41 € |
| 33 | 0 | 10 000,00 € | 50 031,89 € | 2 382,47 € | 40 031,89 € |
| 34 | 0 | 10 000,00 € | 52 533,48 € | 2 501,59 € | 42 533,48 € |
| 35 | 0 | 10 000,00 € | 55 160,15 € | 2 626,67 € | 45 160,15 € |
Les Intérêts Composés
Pour avoir une définition plus claire : Les intérêts composés sont des intérêts calculés sur le capital initial et sur les intérêts accumulés des périodes précédentes. C’est une méthode puissante pour faire croître votre investissement de manière exponentielle.
Imaginez que vous plantez un arbre qui non seulement grandit chaque année, mais qui produit aussi des graines qui deviennent de nouveaux arbres. Chaque année, vous avez plus d’arbres, et chaque arbre produit encore plus de graines, ce qui finit par vous donner une forêt entière, tout ça en ayant planté un seul arbre. C’est exactement ce qui se passe avec les intérêts composés.
Calcul des intérêts composés
où :
- \( C_n \) : est la valeur du capital à l’année \( n \)
- \( C_0 \) : est la valeur du capital initial
- \( r \) : est le taux d’actualisation
- \( x \) : le nombre de fois où l’intérêt est composé par an (par exemple : 1 fois si intérêt composé annuellement ou 12 fois si intérêt composé mensuellement)
- \( n \) : le nombre de périodes (généralement des années)
Continuons avec notre exemple et admettons que vous recherchez la valeur de l’année 10.
Booster l’Investissement
On peut même aller plus loin et ajouter du capital pour booster l’investissement. Dans ce cas, ce capital nouvellement ajouté participera au calcul d’intérêts encore plus importants. Par exemple, si vous ajoutez 1 000 € chaque année à votre investissement initial de 10 000 €, la croissance sera encore plus rapide.
Exemple avec Ajout de Capital
Supposons que vous ajoutez 1 000 € chaque année à votre investissement initial de 10 000 € à un taux d’intérêt annuel de 5 %, composé annuellement. Voici comment cela fonctionne :
| Année | Ajout capital | Capital cumulé | Total gain | Intérêt | Intérêt cumulé |
| 1 | 1000 € | 11 000,00 € | 11 550,00 € | 1 550,00 € | 1 550,00 € |
| 2 | 1000 € | 12 000,00 € | 13 177,50 € | 1 627,50 € | 3 177,50 € |
| 3 | 1000 € | 13 000,00 € | 14 886,38 € | 1 708,88 € | 4 886,38 € |
| 4 | 1000 € | 14 000,00 € | 16 680,69 € | 1 794,32 € | 6 680,69 € |
| 5 | 1000 € | 15 000,00 € | 18 564,73 € | 1 884,03 € | 8 564,73 € |
| 6 | 1000 € | 16 000,00 € | 20 542,96 € | 1 978,24 € | 10 542,96 € |
| 7 | 1000 € | 17 000,00 € | 22 620,11 € | 2 077,15 € | 12 620,11 € |
| 8 | 1000 € | 18 000,00 € | 24 801,12 € | 2 181,01 € | 14 801,12 € |
| 9 | 1000 € | 19 000,00 € | 27 091,17 € | 2 290,06 € | 17 091,17 € |
| 10 | 1000 € | 20 000,00 € | 29 495,73 € | 2 404,56 € | 19 495,73 € |
| 11 | 1000 € | 21 000,00 € | 32 020,52 € | 2 524,79 € | 22 020,52 € |
| 12 | 1000 € | 22 000,00 € | 34 671,55 € | 2 651,03 € | 24 671,55 € |
| 13 | 1000 € | 23 000,00 € | 37 455,12 € | 2 783,58 € | 27 455,12 € |
| 14 | 1000 € | 24 000,00 € | 40 377,88 € | 2 922,76 € | 30 377,88 € |
| 15 | 1000 € | 25 000,00 € | 43 446,77 € | 3 068,89 € | 33 446,77 € |
| 16 | 1000 € | 26 000,00 € | 46 669,11 € | 3 222,34 € | 36 669,11 € |
| … | |||||
| 32 | 1000 € | 42 000,00 € | 126 713,19 € | 7 033,96 € | 116 713,19 € |
| 33 | 1000 € | 43 000,00 € | 134 098,84 € | 7 385,66 € | 124 098,84 € |
| 34 | 1000 € | 44 000,00 € | 141 853,79 € | 7 754,94 € | 131 853,79 € |
| 35 | 1000 € | 45 000,00 € | 149 996,48 € | 8 142,69 € | 139 996,48 € |
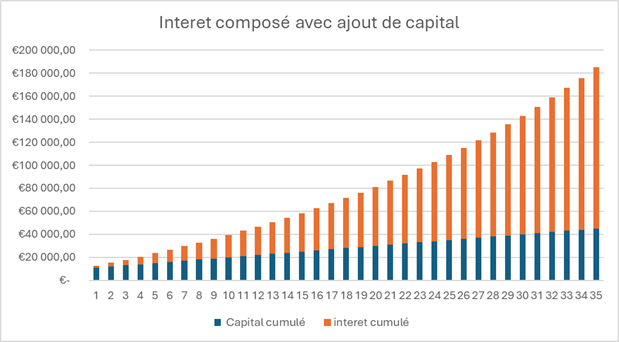
Dans ce cas, à la 11e année, le montant des intérêts devient supérieur au capital cumulé, ce qui devrait finir de vous convaincre de la puissance des intérêts composés, surtout avec l’ajout régulier de capital.
Retenez ceci : la capitalisation et les intérêts composés sont des concepts fondamentaux en finance qui permettent de maximiser la rentabilité à long terme. En réinvestissant les gains et en ajoutant régulièrement du capital, vous pouvez faire croître votre investissement de manière exponentielle. Comprendre et appliquer ces principes peut transformer un investissement modeste en une source de richesse significative au fil du temps.